How non-formal mathematics can be incorporated in the official school curricula
As THEAMA project is dealing with non-formal mathematics it is important to see how they can be incorporated in the official school curricula. Here the terminology non formal and informal mathematics are going to be used interchangeably as any activity not within the official school curricula.
Based on Koedinger & Nathan (2004) the procedures that do not rely on formalisms of mathematics for example symbolic equation are considered as informal procedures for solving mathematics problems and are not necessarily acquired through classroom instruction (Koedinger & Nathan, 2004). Generally, for building mathematical knowledge it is considered to be beneficial for informal procedures and more formal procedures to be combined.
It would have been an omission not to mention that non-formal mathematics can play an important role in any learner’s pathway. From kindergarten to university there are studies supporting this view. For as young as 3-7 years old, gamification -play- can be a mean of smooth transitioning from the child’s informal activities to formal classroom activities. According to research data (Ascher, 2001; Barta & Schaelling, 1998; Ceglowski, 1997; Ernest, 1986; Williams, 1986), gamification -play- seems to be one of the most effective ways to approach mathematics for the younger ages. For older students, as Baroody and Ginsburg (1986) argued, informal mathematics cab be a strong foundation for learning formal mathematics. More specifically, it is stated by Hattikudur, Sidney and Alibaba (2016) -having as their sample university students- that for learners who do not like mathematics; instruction that includes support for comparisons between the formal and informal procedures lead to better results in conceptual knowledge.
A visualization that is strongly related with the framework of THEAMA project can be seen in Kolb’s circle shown below. Kolb’s circle is one of the most popular models that show the relationship between experience, reflection, conceptualization and experimentation. It is based on the idea that some people need to start from a concrete situation, a motivating challenge to put in motion a personal learning development, which should cross the phases shown below to be merged and to introduce a new search or understanding.
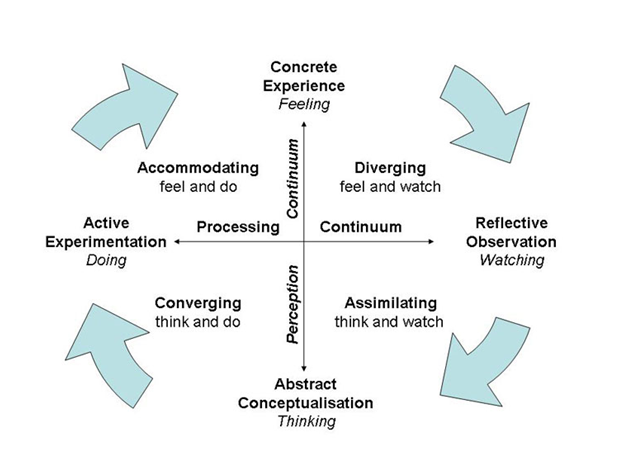
THEAMA project is intending through non-formal mathematics, by providing 54 equally well structured tools-coming from five different sectors; cinematography, drama, music, literature and visual arts- the online gaming, e-resources and a handbook, to give this concrete experience to the learners. It is also giving the opportunity for children ages 13-18 to feel and watch. THEAMA tools give students the material to watch and feel whilst through the examples and tasks given the student is going through the phases of ‘Assimilating’, ‘Converging’ and ‘Accommodating’. This experience given through the THEAMA tools can be acquired within the classroom, or at home, through group lessons or individually wherever and by whoever wants to pact with mathematics. It is offered to learners as an Open Educational Resource online thus anyone can use this non formal approach to their benefit.
We will conclude with the thought that aspired this project and it was perfectly stated by MMACA (Musee de Mathematique de Catalunya):
“There are two kinds of people: those who love maths and those that have not yet found out they love it”
THEAMA wishes to elevate the former group’s love and stimulate the latter.
References
Baroody, A. J., & Ginsburg, H. P. (1986). The relation between initial meaningful and mechanical knowledge of arithmetic. In J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 75–112). Hillsdale, NJ: Erlbaum Associates.
Barta, J. & Schaelling, D. (1998). Games we Play: Connecting Mathematics and Culture in the Classroom. Teaching Children
Ceglowski, D. (1997). Understanding and Building upon Children’s Perceptions of Play Activities in Early Childhood Programs Early Childhood Education Journal, 25(2): 107-112.
Ernest, P. (1986). Games a rationale for their use in the teaching of mathematics in school Mathematics in School Vol. 15, No 1
Hattikudur, Shanta; Sidney, Pooja G.; and Alibali, Martha W. (2016) “Does Comparing Informal and Formal Procedures Promote Mathematics Learning? The Benefits of Bridging Depend on Attitudes Toward Mathematics,” The Journal of Problem Solving: Vol. 9 : Iss. 1 , Article 2.
DOI: 10.7771/1932-6246.1180
Koedinger, K. R., & Nathan, M. J. (2004). The real story behind story problems: Effects of representation on quantitative reasoning. Journal of the Learning Sciences, 13, 129–164. http://dx.doi.org/10.1207/s15327809jls1302_1
Williams, M. (1986). The Place of Games in Primary Mathematics Mathematics in School Vol.15, No 1 (pp. 19)

This project has been funded with support from the European Commission. This website and all its contents reflect the views only of the author, and the Commission cannot be held responsible for any use which may be made of the information contained therein.
[Project number: 2018-1-SE01-KA201-039031]










